Introduction to Cosine Similarity
Comparing texts by context and their similarity will fail if we use only simple calculations of counting the maximum number of common words between documents. Cosine similarity is a metric used to determine how similar the documents are, irrespective of their size.
When document size increases, the number of common words tends to increase even if the documents refer to different topics. The cosine similarity helps to overcome this fundamental flaw in the “count the common words” or Euclidean distance approach.
Pre-Processing in NLP and Vectorization
An important part of NLP, or any language AI model, is pre-processing data, words, and sentences into vectors, or a process called token embedding.
Once vector outputs are well structured, the transformer, which is usually a matrix of high number dimensions, can be 40,000 dimensions, is used to calculate the next move and step forward in neural networks, in a very simplistic way to describe it.
Having the right input in vectorized operations is key; you cannot have a great model without understanding what to do with the data, and magic is often in the way you vectorize input, not how to manipulate the transformer.
Transformers, calculated based on vector covariance, are symmetrical because the distance from point A to point B in Euclidean space is the same as the distance from B to A.
This, however, may not be the same for Minkowski’s space of the special theory of relativity, where an object moving with speed is a factor of length contraction.
Challenges with Time Series Data in NLP
One can deduce that NLP fails very fast on time series data, where we need inputs and transformers to accommodate time and sequence of events, SIGINT, somehow. Transformers matrices can be independently studied as their own manifold, with laws of movement, imaging almost like language flow as a river with waves, as a very simplistic explanation.
Cosine Similarity Formula and Distance
The formula is:
It is important to note that A and B are vectors; therefore, A . B is a scalar product, often called the dot product, while ||A|| = norm of the vector, in Euclidean space, is simply Pythagoras’ theorem.

Is important to define now distance, called Cosine Distance, meaning between two unit-length vectors A and B:
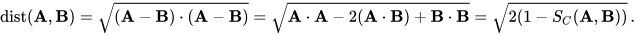
Nonetheless, the cosine distance is often defined without the square root or factor 2:

This is an important relationship, as we have vectors, then measure their relationship and also their distance. So, think of this as mapping for every two vectors. We can assign two new parameters, such as how they are related and how far they are from each other.
Range and Interpretation of Cosine Similarity
The range of values for cosine similarity can be any real number from [-1,1], and edge cases are: 1 – vectors point in the same direction (perfectly similar), 0 – vectors are orthogonal (perpendicular, no similarity), and -1 – vectors point in the opposite direction.
Simple usage is that a document can be represented as a vector or broken into vectors, and the value represents the frequency of that word in the document.
By calculating cosine similarity between two documents, now two vectors, you can determine how similar two documents are based on their shared vocabulary.
Center of Cosine Similarity and Pearson Correlation
An important question would be where is the center for the cosine similarity of two vectors, meaning the equilibrium state based on two vectors. This leads to the Pearson correlation coefficient, which reflects covariance and standard deviation.
Stein Paradox and Vector Parameters
The Stein paradox also plays a significant role in quantifying vector parameters, such as the mean value. Gaus demonstrated that the sample mean maximizes the likelihood of observing the data, making it an unbiased estimator, meaning it doesn’t systematically overestimate or underestimate the true mean.
Researchers like R.A. Fisher and Jerzy Neyman introduced risk functions while expanding on the idea mean through minimization of the expected square errors compared to other linear unbiased estimators.
When we have more than three parameters simultaneously, the sample mean becomes inadmissible. In such vector fields, biased estimators can outperform the sample mean by offering lower overall risk.
James-Stein Estimator and Its Implications
A great explanation of the general formula for the James-Stein estimator can be found here.
X is the sample mean vector, μ is the grand mean, and c is a shrinkage factor that lies between 0 and 1refelecting how much we pull the individual means toward the grand mean.

The goal is to reduce the distance between individual sample means and the grand mean. The James-Stein estimator demonstrates a paradox in estimation: it is possible to improve estimates by incorporating information from seemingly independent variables.
